题目
题目描述
A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different heights. For example, the figure on the left shows the histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3, measured in units where 1 is the width of the rectangles: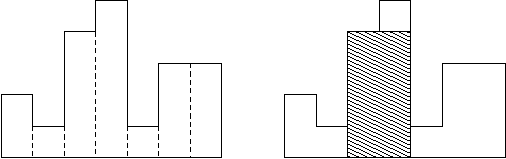
Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.
输入格式
The input contains several test cases. Each test case describes a histogram and starts with an integer n, denoting the number of rectangles it is composed of. You may assume that 1 <= n <= 100000. Then follow n integers h1, …, hn, where 0 <= hi <= 1000000000. These numbers denote the heights of the rectangles of the histogram in left-to-right order. The width of each rectangle is 1. A zero follows the input for the last test case.
输出格式
For each test case output on a single line the area of the largest rectangle in the specified histogram. Remember that this rectangle must be aligned at the common base line.
输入样例
1 | 7 2 1 4 5 1 3 3 |
输出样例
1 | 8 |
题解
部分内容来自李煜东所著《算法竞赛进阶指南》
如果说这道题矩形的高度是递增的,估计就是一道普及难度的题了吧。
我们可以尝试以每个矩形的高度作为最终矩形的高度,并将宽度扩展到右边界,答案取最大值。
简单归简单,不过这也给了我们一个启发,如果是递增的我们就放着不管,以后来处理。如果说下一个高度更小,那么用它所构成的矩形的高度不可能超过它自己,而后面的矩形想要和前面的矩形拼接的话,高度也不能超过它。
这样子的话,我们就可以用上面的方法更新比当前矩形高的矩形的答案再将它们合并。
这就是单调栈算法,时间复杂度 $ O(N) $
借助单调性处理问题的思想在于及时排除不可能的选项,保持策略集合的高度有效性和秩序性
就这拿道题举例,我们建立一个栈,用来保存若干个矩形,这些矩形的高度是单调递增的,或者说,我们期望他是单调递增的。
我们从左到右读入矩形:
如果当前矩形比栈顶矩形高,即满足单调递增,进栈。
否则不断去除栈顶,直至栈空或栈顶高度低于当前矩形。在此过程中,我们累计被弹出的矩形的宽度和(用于计算答案与合并),用高度×累计宽度更新答案。而后,将一个宽度为累计宽度,高度为当前矩形的矩形入栈。
结束,将剩余矩形弹出,和上面一样更新答案;
代码
1 |
|